Flow estimation

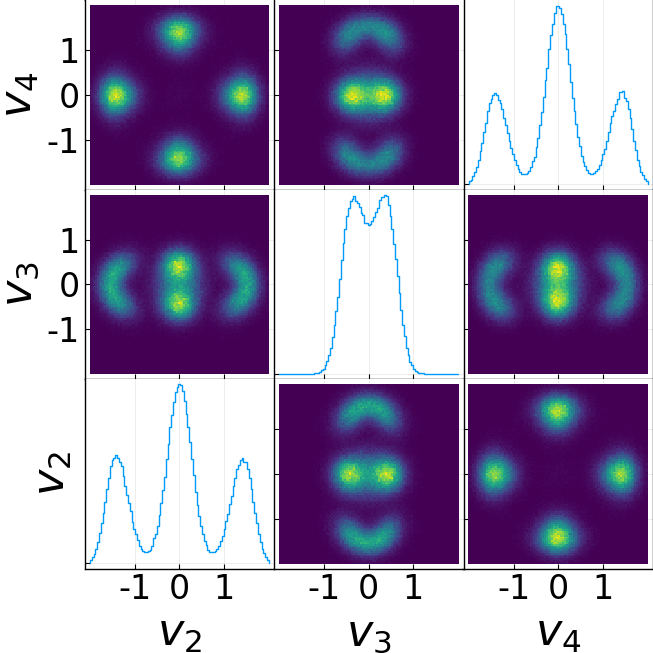
The goal of this project was to estimate a fluid flow from (noisy, finite) observations of a solute (e.g., a pollutant or dye) advecting and diffusing in the fluid. Here the goal was to estimate incompressible flow \(\mathbf{v}\) from observations of solute concentration \(\theta\) governed by the two-dimensional advection-diffusion equation: \(\frac{\partial}{\partial t} \theta = -\mathbf{v} \cdot \nabla \theta + \kappa \Delta \theta\)

This problem was sort of a playground to test out the framework for Bayesian inversion for infinite-dimensional unknowns, as well as Markov Chain Monte Carlo methods designed for those applications, from perspectives ranging from the highly computational (GPU-based algorithms) to the highly theoretical (long proof-based paper).

Relevant Publications:

• Glatt-Holtz, Nathan E, Andrew J Holbrook, Justin A Krometis, and Cecilia F Mondaini. “Parallel MCMC Algorithms: Theoretical Foundations, Algorithm Design, Case Studies.” Transactions of Mathematics and Its Applications 8, no. 2 (December 1, 2024): tnae004. https://doi.org/10.1093/imatrm/tnae004.
• Borggaard, Jeff, Nathan Glatt-Holtz, and Justin Krometis. “On Bayesian Consistency for Flows Observed Through a Passive Scalar.” Annals of Applied Probability 30, no. 4 (2020): 1762–83. https://doi.org/10.1214/19-AAP1542.
• Borggaard, Jeff, Nathan Glatt-Holtz, and Justin Krometis. “A Bayesian Approach to Estimating Background Flows from a Passive Scalar.” SIAM/ASA Journal on Uncertainty Quantification 8, no. 3 (January 2020): 1036–60. https://doi.org/10.1137/19M1267544.
• Borggaard, Jeff, Nathan Glatt-Holtz, and Justin Krometis. “GPU-Accelerated Particle Methods for Evaluation of Sparse Observations for Inverse Problems Constrained by Diffusion PDEs.” Journal of Computational Physics, 2019. https://doi.org/10.1016/j.jcp.2019.04.034.